Метод аналізу ієрархій (МАІ) – математичний інструмент системного підходу до вирішення складних проблем прийняття рішень. Основне застосування методу полягає в підтримці прийняття рішень за допомогою ієрархічної композиції завдання та рейтингування альтернативних рішень.

Цей метод розроблений американським математиком Томасом Сааті, який написав про нього книги, розроблював програмні продукти і протягом 20 років проводив симпозіуми ISAHP (англ. International Symposium on Analytic Hierarchy Process).

Ви можете скористатись сервісом для цього методу за посиланням.

МАІ широко використовується на практиці і активно розвивається вченими всього світу. У його основі поряд з математикою закладені і психологічні аспекти. МАІ дозволяє зрозумілим і раціональним чином структурувати складну проблему прийняття рішень у вигляді ієрархії, порівняти і виконати кількісну оцінку альтернативних варіантів рішення. Метод аналізу ієрархій використовується у всьому світі для прийняття рішень в різноманітних ситуаціях: від управління на міждержавному рівні до розв’язання галузевих і приватних проблем в бізнесі, промисловості, охороні здоров’я і освіті. Велика частина відомих СППР в якості теоретичної основи використовує метод аналізу ієрархій, який широко застосовується в практиці прийняття рішень.

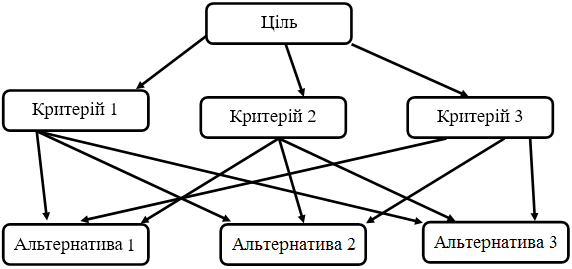
Ієрархія – система, в якій рівні розташовані та пронумеровані так, що:

  1. нижній рівень містить рейтинговані альтернативи;
  2. вузли з вищих рівнів можуть домінувати тільки над вузлами нижчих рівнів.


Таким чином, в ієрархії зв’язки визначають шляхи однієї спрямованості – від вершини до альтернатив через проміжні рівні, які складаються з вузлів-критеріїв:

Основні етапи методу аналізу ієрархій

Етап 1. Побудова ієрархічної структури задачі.

Аналіз проблеми прийняття рішень в МАІ починається з побудови ієрархічної структури, яка включає мету, критерії, альтернативи й інші фактори, що впливають на вибір. Кожен елемент ієрархії може представляти різні аспекти задачі, що розв’язується, причому до уваги можуть бути прийняті як матеріальні, так і нематеріальні чинники, вимірювані кількісні параметри та якісні характеристики, об’єктивні дані і суб’єктивні експертні оцінки:

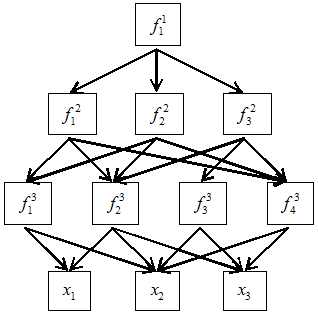
Де – елементи ієрархії критеріїв, верхній індекс елементів вказує рівень ієрархії, нижній – порядковий номер; – альтернативи.

Етап 2. Визначення пріоритетів елементів ієрархічної структури.

Наступним етапом аналізу є визначення пріоритетів, що представляють відносну важливість або перевагу елементів побудованої ієрархічної структури, за допомогою процедури парних порівнянь.

Безрозмірні пріоритети надають можливість обґрунтовано порівнювати різнорідні фактори, що є відмінною особливістю МАІ.

Для встановлення відносної важливості  елементів ієрархії використовується шкала відношень Сааті. Ця шкала надає експерту можливість ставити у відповідність ступеням переваги одного фактору перед іншим – деяке число.

Таблиця – Шкала відношень
(ступеня значимості дій)
Ступінь значимості Визначення Пояснення
1 Однакова значимість Дві дії мають однаковий внесок у досягнення мети
3 Слабка значимість Існують не достатньо переконливі міркування на користь переваги однієї з дій
5 Істотна значимість Маються надійні дані для того, щоб показати перевагу однієї з дій
7 Очевидна значимість Переконливе свідчення на користь однієї дії перед іншою
9 Абсолютна значимість Незаперечні переконливі свідчення на користь переваги однієї дії перед іншою
2,4,6,8 Проміжні значення між сусідніми судженнями Ситуація, коли необхідне компромісне рішення

Правомірність цієї шкали доведена практично при порівнянні з багатьма іншими шкалами. При використанні зазначеної шкали експерт, порівнюючи два об’єкти в змісті досягнення цілі, розташованої на вищому рівні ієрархії, повинен поставити у відповідність цьому порівнянню число в інтервалі від 1 до 9 або обернене до нього. У тих випадках, коли важко розрізнити скільки є проміжних градацій від абсолютної до слабкої переваги або цього не потрібно в конкретній задачі, може використовуватися шкала з меншим числом градацій. Гранично шкала має дві оцінки: 1 – об’єкти рівнозначні; 2 – перевага одного об’єкта над іншим.

Після побудови ієрархії використовується метод порівняння її елементів. Якщо приймається метод попарного порівняння, то будується множина матриць попарних порівнянь. Для цього в ієрархії виділяють елементи двох типів: елементи – “батьки” і елементи – “нащадки”. Елементи – “нащадки” впливають на відповідні елементи вищого рівня ієрархії, які є для них “батьками”.

Матриці попарних порівнянь будуються для всіх елементів – “нащадків”, що відносяться до відповідного елемента – “батька”. Елементами – “батьками” можуть бути елементи, що належать будь-якому ієрархічному рівневі, крім останнього, на якому розташовані, як правило, альтернативи.

Матриця попарних порівнянь заповнюється за наступним правилом:

Етап  3.  Знаходження вектору пріоритетів

Ранжування елементів, що аналізуються з використанням матриці попарних порівнянь, здійснюється на підставі аналізу головних власних векторів матриці попарних порівнянь. Власний вектор забезпечує упорядкування пріоритетів, а власне значення є мірою узгодженості (однорідності) суджень. Обчислення головного власного вектору W додатної квадратної матриці А проводиться на підставі рівності:

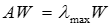
Де 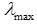– максимальне власне число матриці А,

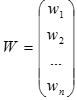– головний власний вектор матриці А.

Якщо власний вектор W нормований (сума його елементі дорівнює 1), то він є вектором пріоритетів для матриці А.

Якщо власний вектор W ненормований, то потрібно його пронормувати. Для цього необхідно знайти суму всіх його елементів і утворити новийвектор W’, елементи якого є відношенням елементів вектору W на знайдену суму:

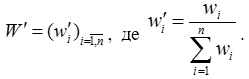
Для додатної квадратної матриці А правий власний вектор W, що відповідає максимальному власному числу 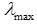з точністю до постійного множника С, можна обчислити за формулою:

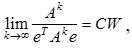
Де 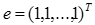– одиничний вектор; k – показник ступеня.

На практиці обчислення власного вектору виконуються до досягнення заданої точності:

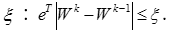
За достатню для практики точність можна прийняти 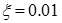незалежно від порядку матриці. Максимальне власне значення обчислюється за формулою:

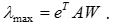
При розробці СППР “Decisioner” використано модифікований метод, який заключається в тому, що при точному процесі визначення вектора локальних пріоритетів задача зводиться до знаходження власного вектора матриці парних порівнянь. Шуканим є вектор, який відповідає максимальному власному значенню. Вектор локальних пріоритетів може бути наближено обчислений спрощеним способом.

3.1 Для кожного рядка матриці парних порівнянь знаходимо середнє геометричне її елементів:

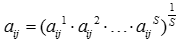
3.2 Знаходимо суму всіх середніх геометричних.
3.3 Ділимо кожне середнє геометричне на їх суму (нормування). Результат – вектор локальних пріоритетів даної матриці.

Етап 4. Оцінювання узгодженості (однорідності) суджень експертів.

При порушенні однорідності ранг матриці буде відмінний від одиниці і вона буде мати кілька власних значень. Однак при невеликих відхиленнях суджень від однорідності одне з власних чисел буде істотно більшим за інші і приблизно дорівнюватиме порядкові матриці. Таким чином, для оцінювання однорідності (узгодженості) суджень експерта необхідно використовувати відхилення величини максимального власного числа від порядку матриці n.

Відомо, що узгодженість квадратної додатної обернено-симетричної матриці еквівалентна вимозі рівності її максимального власного значення 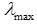числу n. Можна також оцінювати відхилення від узгодженості різницею 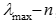поділеною на (n−1). Зауважимо, що нерівність 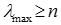завжди має місце. Наскільки погана узгодженість для певної задачі, можна оцінити шляхом порівняння одержаного значення величини 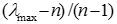з значенням з випадково обраних суджень і відповідних обернених величин матриці того ж розміру. Однорідність (узгодженість) суджень експертів оцінюється індексом однорідності (ІО), що дорівнює:

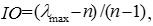
або відношенням однорідності (ВО), що дорівнює:

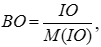
де М(ІО) – середнє значення (математичне сподівання) індексу однорідності випадковим чином складеної матриці попарних порівнянь по шкалі від 1 до 9 обернено-симетричної матриці з відповідними оберненими величинами елементів, що базується на експериментальних даних таблиці:

Етап 5. Ієрархічний синтез.

Ієрархічний синтез використовується для зважування власних векторів матриць попарних порівнянь альтернатив вагами критеріїв (елементів), що знаходяться в ієрархії, а також для обчислення суми за всіма відповідними зваженими компонентами власних векторів нижчого рівня ієрархії. Далі розглядається алгоритм ієрархічного синтезу з урахуванням позначень, прийнятих у ієрархії.

Крок 1. Визначаються вектори пріоритетів альтернатив 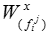щодо елементів передостаннього рівня ієрархії (i=S). Тут через позначені елементи ієрархії, причому верхній індекс і указує рівень ієрархії, а нижній індекс j – порядковий номер елемента на рівні. Обчислення множини векторів пріоритетів альтернатив щодо рівня ієрархії S здійснюється за ітераційним алгоритмом, реалізованим на основі співвідношень обрахунку головного пронормованого вектору W по вихідним даним, зафіксованим у матрицях попарних порівнянь. У результаті визначається множина векторів:

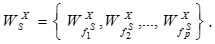
Крок 2. Аналогічним образом обробляються матриці попарних порівнянь власне елементів . Дані матриці, побудовані таким чином, щоб визначити перевагу елементів визначеного ієрархічного рівня щодо елементів вищого рівня, з якими вони безпосередньо зв’язані.

У результаті обробки матриць попарних порівнянь визначається множина векторів пріоритетів критеріїв:

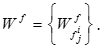
Отримані значення векторів використовуються згодом при визначенні векторів пріоритетів альтернатив щодо всіх елементів ієрархії.

Крок 3. Здійснюється власне ієрархічний синтез, що полягає в послідовному визначенні векторів пріоритетів альтернатив щодо критеріїв , які знаходяться на всіх ієрархічних рівнях, крім передостаннього, що містить критерії . Обчислення векторів пріоритетів проводиться в напрямку від нижніх рівнів до верхнього з урахуванням конкретних зв’язків між критеріями, що належать різним рівням. Обчислення проводиться шляхом перемножування відповідних матриць і векторів.

Загальний вид виразу для обчислення векторів пріоритетів альтернатив визначається таким способом:

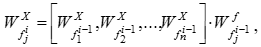
Де – вектор пріоритетів альтернатив щодо критерію , що визначає j –й стовпчик матриці; – вектор пріоритетів критеріїв , зв’язаних з критерієм вищого рівня ієрархії.