Метод аналізу співвідношень (англ. MOORA – Multiobjective Optimization On the basis of Ratio Analysis) запропонували В. Карел, М. Брауерс, Е. Завадскас, Ф. Пельдшус та С. Турскіс в роботі у 2008 році.
Метод аналізу співвідношень (MOORA) складається з двох частин:
- побудова системи співвідношень;
- обчислення наближення до точки відліку.
Значення показника метрики s вибирається в залежності від предметної області, до якої відноситься поставлена задача. На практиці використовуються значення s = 1, 2, ∞. Якщо значення s = 2, то маємо евклідовий m-вимірний метричний простір. Його обирають у випадках, коли критерії мають зміст відстані чи інших фізичних величин, для яких евклідова метрика є змістовною.
Визначимо відстань між точками у і a у метричних просторах з показником метрики s ≥ 1:
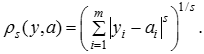
Побудова системи співвідношень починається з побудови матриці відношень різних альтернатив до різних критеріїв (цілей):
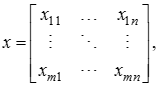
де хij (і = 1, m; j = 1, n) – відношення альтернатив і до критеріїв (цілі) j.
Система співвідношень в методі MOORA, це система, у якій кожне відношення альтернативи до цілі порівнюється зі знаменником, який представляє собою суму всіх відношень альтернатив до цієї цілі.
Для цього знаменника найкращим вибором буде квадратний корінь з суми квадратів відношення кожної альтернативи до цілі:
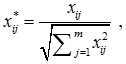
де – відношення альтернативи
j до цілі i; j = 1,…,m; m – кількість
альтернатив; i = 1,…,n, n – кількість цілей;
– безвимірне число, що представляє
нормоване відношення альтернативи j до цілі i.
Для оптимізації, такі реакції будуть додані в разі максимізації та відняті при мінімізації:
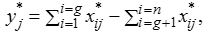
де i = 1,2,…, g – цілі, що мають бути максимізовані; i = g + 1, g + 2,…,n – цілі, що мають бути зведені до мінімуму; – нормована оцінка варіанту j з врахуванням всіх цілей. Порядкове ранжування
показує остаточний вибір. Головні ваги можуть
бути порівняні з порядковим ранжуванням.
Метод аналізу співвідношень допомагає отримати рекомендації щодо оптимального прийняття рішення за компактним, але ефективним алгоритмом.
